0 引言
物体的状态,通常指一组可以描述其随时间变化的物理量[1],例如位置、速度、加速度以及角度等。状态估计问题拥有很长的历史,早在几千年前,航海家就面临对船只在海洋中的位置进行估计的问题,这些需求激励了测量技术的发展。
状态估计理论的起源可以追溯至1654年帕斯卡和费马奠定了概率论的基础,以及1764年贝叶斯法则的提出。1801年,高斯利用最小化观测误差提出了最小二乘法,成功估计出了谷神星的轨道,并于1803年证明了在观测噪声为正态分布的条件下,最小二乘估计就是最优估计。到20世纪中期,卡尔曼1960年发表的文章[2]为状态估计理论的发展指明了方向,这种针对高斯线性系统的经典状态估计方法就是卡尔曼滤波,可以证明,卡尔曼滤波是对高斯线性系统的最优线性无偏估计。基于卡尔曼滤波的思想,通过引入线性化手段,适用于非线性系统高斯噪声下的扩展卡尔曼滤波(Extended Kalman Filter,EKF)、无迹卡尔曼滤波(Unscented Kalman Filter,UKF)和容积卡尔曼滤波(Cubature Kalman Filter,CKF)算法被陆续提出。此外,20世纪后期提出的粒子滤波、最大后验估计、贝叶斯估计等状态估计方法,将状态估计的应用领域扩展至了非线性系统。
上述状态估计方法均建立在一对一观测模型的基础上,即单个传感器对单一目标进行状态估计,而这样的结构虽然能实现对动态目标的最优或次优估计,但抗干扰能力不强,鲁棒性较差;于是,使用多个传感器对同一目标进行融合状态估计的思路开始受到研究人员的关注[3,6-7],这就是多传感器融合状态估计研究的起点。2004年之前,多传感器分布式状态估计的研究处于起步期[12-14];得益于网络一致性算法这一强有力工具的提出[31-32],分布式状态估计得到了蓬勃发展[34-36]。本文依照由集中式到分散式再到分布式状态估计的发展顺序,对分布式状态估计的发展进行梳理。
第1章介绍了集中式状态估计方法。在以高斯线性系统为研究对象时,卡尔曼滤波是最小均方误差准则下的最优估计(对于非线性系统,可在滤波层面使用EKF、CKF、粒子滤波等非线性滤波方法,不影响集中式状态估计的架构)。因此,第1章详细总结了基于观测融合的集中式卡尔曼滤波方法,作为全局最优的比较基准。
第2章以多传感器数据融合中的相关数据的融合问题为焦点,总结了由集中式到分散式与分布式状态估计发展过程中的经典方法。
第3章总结了一致性算法出现后的分布式状态估计方法,主要有估计一致性、测量一致性和信息一致性等方法,并讨论了这些方法的最优性和分布式水平。此外,指出了信息一致性方法分布式地实现了第2章中状态向量融合的无偏保守估计。
1 集中式状态估计
本章首先介绍了多传感器融合状态估计中最早提出且最直接的思路,即集中式状态估计方法。在高斯线性系统的最小均方误差准则下,使用集中式卡尔曼滤波得到融合状态估计结果,是分布式状态估计的精度上限和比较基准。
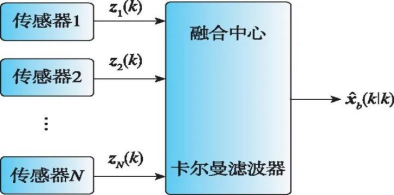
引言中提到,单一传感器向多传感器状态估计推广能够提升状态估计精度,增强系统的鲁棒性。较为直观的思路是,收集多个传感器对目标的观测,集中执行状态估计。麻省理工大学的D.Willner等[3]在1976年的文章中提出了适用于多传感器系统的卡尔曼滤波算法,将多个传感器的观测合成为一个向量再进行卡尔曼滤波,可实现全局最小均方误差估计,这种方法也因此被称作集中式卡尔曼滤波。设l个传感器对系统状态随机向量的观测方程为
zk+1,i=hi(xk+1)+vk+1,i (1)
若所有传感器的观测数据被同步收集,则有
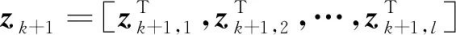 (2)
(2)
在传感器观测噪声互不相关的条件下,观测向量的协方差矩阵为
 (3)
(3)
至此,基于观测融合,D.Willner等提出了三种滤波方法。当系统为线性高斯且传感器同构的情况下,三种方法等价,均为最优估计,第一种方法运算量最大,第三种最小[4]。
1)并行滤波器:这种方法在收集观测数据的中心节点时直接采用卡尔曼滤波对状态向量进行求解,但矩阵维数随传感器数量而增加,导致直接求解计算负荷较大。
2)顺序滤波器:顺序结构的滤波器将收集到的l个传感器的观测数据依次用于卡尔曼滤波的更新中,即下一时刻全局的状态更新需要进行l次卡尔曼滤波。
3)数据压缩滤波器:所谓数据压缩,是指对l个观测向量进行融合后再进行卡尔曼滤波,事实上,这种方法利用了最优加权最小二乘估计对观测向量进行融合
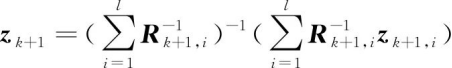 (4)
(4)
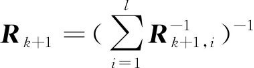 (5)
(5)
得到了压缩的观测向量及相应的协方差矩阵后再进行卡尔曼滤波,但在传感器异构时不可用。在图1所示的集中式融合状态估计架构中,数据关联和时空配准是多传感器融合中的必要步骤,滤波算法在融合中心进行实现。
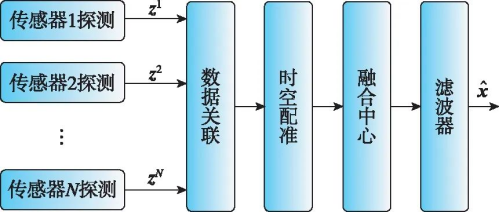
图1 集中式融合状态估计架构
Fig.1 Centralized state estimation structure
由于均需要收集所有传感器的观测,以上三种方法也被称为观测融合(measurement fusion)。这些方法要求每个传感器与中心节点进行通信,对计算量、存储能力以及通信能力的要求较高,并且容错能力较弱。因此,若在每个传感器执行本地估计,利用信息融合的方法实现分布式融合状态估计,可克服集中式状态估计的不足。分布式状态估计开始成为新的研究热点。
需要注意的是,对于高斯线性系统,集中式卡尔曼滤波是最小均方误差意义下的全局最优估计。可以证明,卡尔曼滤波给出的误差协方差矩阵位于克拉美罗下界处,所以卡尔曼滤波是最优线性无偏估计[1](Best Linear Unbiased Estimate,BLUE)。因此,集中式卡尔曼滤波是所有线性无偏状态估计方法中误差比较的基准[33],分布式方法的估计精度不能超越集中式。
2 多传感器数据融合——相关数据的融合方法
在多传感器分布式状态估计的研究进程中,对来自不同传感器的数据进行融合及利用是最基础的问题,而分布式则主要关心如何将融合方法在传感器网络中的每个节点本地实现。2013年,B.Khaleghi等[5]给出了关于多传感器数据融合(Multi Sensor Data Fusion,MSDF)技术的全面回顾,总结了MSDF面临的挑战及其应对方法,包括数据缺陷、数据相关性、数据不一致性等问题,如图2所示。其中,数据相关性问题伴随着MSDF的发展,是最受研究者关切的问题之一。本章聚焦多传感器数据融合中的数据相关性问题,并将在之后的章节中展示分布式状态估计算法是如何解决这一问题的。
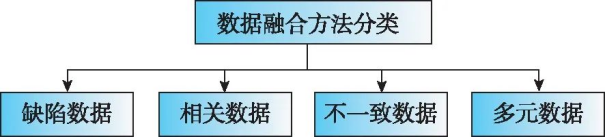
图2 数据融合方法分类Fig.2 Taxonomy of data fusion methods
2.1 有相关性数据的融合——状态向量融合
1971年,R.A.Singer等[6]首次讨论了两个使用卡尔曼滤波的传感器关于同一目标的轨迹跟踪之间的联系(track-to-track association)以及相应的轨迹融合(track fusion)方法,但这种方法建立在假设两个传感器的估计误差之间相互独立的条件上,而在实际中,对同一目标的观测和状态估计过程往往是相关的。Y.Bar-Shalom在1981年[7]对上述两个轨迹之间的关联进行了研究,推导了两个传感器估计误差之间的协方差矩阵,并基于该协方差矩阵在其1986年发表的文章[8]中提出了在最小化融合均方差准则下的两个传感器的最优融合公式,又被称为Bar-Shalom/Campo公式或track-to-track fusion。这种方法通过对状态估计向量的加权实现传感器数据融合,为已知误差相关性的多传感器融合估计提供了思路,这种方法也被称为状态向量融合(state-vector fusion)。假设两个传感器对同一目标的状态估计分别为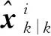 和
和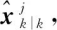 引入卡尔曼滤波的线性最小方差估计的思想
引入卡尔曼滤波的线性最小方差估计的思想
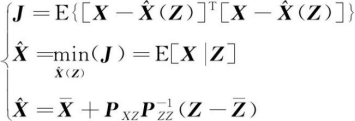 (6)
(6)
将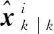 视作由先验得到的状态预测,将
视作由先验得到的状态预测,将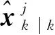 视作是观测用于修正预测,则可得
视作是观测用于修正预测,则可得
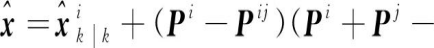
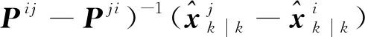 (7)
(7)
其中,Pi、Pij分别为传感器i的估计误差方差矩阵和传感器i、j估计误差之间的交叉协方差矩阵。上述融合结果可以写为如下形式
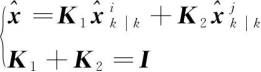 (8)
(8)
综上所述,这种状态向量融合的方法可以在已知估计误差相关性的情况下,以最小均方差为准则融合两个传感器的状态估计。文献[9]通过仿真实验对比了第1章介绍的集中式卡尔曼滤波的观测融合与上述状态向量融合方法的性能表现,说明了状态向量融合方法的估计误差始终高于集中式的观测融合方法。因此,这种状态向量融合方法并不是最优的,而被证明是一种次优估计[10],相比集中式状态估计,其优势在于更低的计算负荷以及可被用于分布式结构的状态估计。由于观测融合与状态向量融合方法均受卡尔曼滤波思想的启发,在后续的研究中,这两种状态向量融合方法也被归为KF(Kalman Filter)融合方法[11]。
2004年,S.L.Sun等[12]基于矩阵加权线性最小融合方差,推导出了在这一准则下的多传感器最优信息融合方法,可看作是Bar-Shalom/Campo公式在多传感器数据融合下的推广。假设对同一个n维随机向量x有l个无偏估计
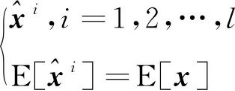 (9)
(9)
估计误差为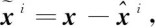 有误差方差矩阵pii。且对于任意的
有误差方差矩阵pii。且对于任意的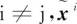 与
与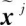 存在相关性,有误差交叉协方差矩阵Pij。设融合公式
存在相关性,有误差交叉协方差矩阵Pij。设融合公式
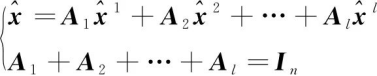 (10)
(10)
为待定系数矩阵的最优无偏融合估计,根据无偏估计的性质,加权矩阵的和等于单位矩阵。则融合后的误差协方差矩阵为
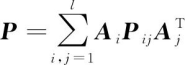 (11)
(11)
为了最小化式(11)所示的误差协方差矩阵的迹,本文通过拉格朗日乘子法给出了最优加权矩阵以及相应的误差协方差矩阵
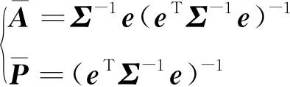 (12)
(12)
其中,e=[In,…,In]T, Σ=(Pij)nl×nl。事实上,Sun等对多传感器加权融合后的误差协方差矩阵的迹进行的最小化方法,与Y.Bar-Shalom等对两个传感器采用的卡尔曼滤波融合方法等价,这是由于式(6)所示的估计误差方差与式(11)中误差协方差矩阵的迹是相同的。
Sun等由此提出了分布式传感器信息融合的双层融合结构,第一层用于计算任意两个传感器估计误差之间的协方差矩阵,第二层进行权重的计算与数据融合。也就是说,这种方法需要每个传感器能够对网络中的其他传感器进行点对点广播通信;并且需要获取每个传感器间的相关性,通信量和运算量随着传感器数量的增加而呈指数增长,可扩展性不强。
在文献[10]中,Chang K.C.等分析了Y.Bar-Shalom等提出的状态向量融合是次优估计的原因,即在基于传感器i的观测数据预测传感器j的状态估计时,假设其与传感器i的状态估计是相同的。通过贝叶斯方法推知,这样假设背后的隐含条件是
p(x|Dj)=p(x|Di,Dj) (13)
这意味着Di⊂Dj,其中,Di和Dj分别是传感器i与传感器j的累积观测数据,显然该假设是不合理的。同时,Chang K.C.等还指出,这种状态向量融合方法是缺少先验信息时的最大似然估计,因此是一种次优估计。
此外,Chang K.C.等还分析了Chong C.Y.于1979年[13]提出的一种层次估计方法,也被称为基于信息融合的方法能够做到分布式的全局最优估计,其具体形式如下
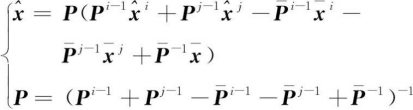 (14)
(14)
其中,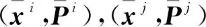 和
和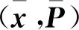 分别为两个传感器各自的先验信息以及融合估计的先验。因此,这种方法要求传感器之间保持高速率的通信,实时将自身的先验及状态估计发送给网络中的其他传感器。因此,这种方法的通信负荷很大,一旦通信实时度下降或先验信息不完全,将退化为次优估计。文献[10]通过蒙特卡罗仿真实验,验证了该方法在高速率通信的条件下可以实现与集中式观测融合方法相近的最优估计误差,误差低于状态向量融合方法;但当通信频率下降时,且误差可能高于状态向量融合方法。几种融合方法总结如表1所示。
分别为两个传感器各自的先验信息以及融合估计的先验。因此,这种方法要求传感器之间保持高速率的通信,实时将自身的先验及状态估计发送给网络中的其他传感器。因此,这种方法的通信负荷很大,一旦通信实时度下降或先验信息不完全,将退化为次优估计。文献[10]通过蒙特卡罗仿真实验,验证了该方法在高速率通信的条件下可以实现与集中式观测融合方法相近的最优估计误差,误差低于状态向量融合方法;但当通信频率下降时,且误差可能高于状态向量融合方法。几种融合方法总结如表1所示。

表1 几种多传感器数据融合方法比较
Tab.1 Comparison of several MSDF methods
综上所述,本文介绍的对于线性高斯系统的多传感器融合方法中,集中式的观测融合方法1)可以实现全局的线性最小方差估计,是一种最优估计,但矩阵维数高,计算量大;观测融合方法2)、3)在传感器同构时与方法1)等价,并且能够降低计算量。状态向量融合方法是一种次优无偏估计,实现了多个传感器状态估计向量加权时的最小方差,被文献[10]证明是最大似然意义下的最优,并非全局最小均方差;但这种方法计算量小,可实现分布式的融合架构。此外,还有学者对状态向量融合进行了改进[11],将融合后的状态估计用于下一时刻所有传感器的预测步,而不再用各自传感器融合前的状态估计,在异构传感器网络中取得了更好的表现。信息融合方法采用所有传感器的先验信息及状态估计信息,在高速率通信时可以实现最优估计,从融合形式上看,也是一种广义的状态向量融合(状态估计向量及其先验);但该方法通信量大,计算量大,通信实时度下降时将退化为次优估计。此外,N.A.Carlson[41]提出的联邦滤波器也是多传感器融合状态估计中重要的学术贡献,通过将状态向量划分为公共状态和专有状态,能够解决异质传感器网络下的融合状态估计,在大类上也是一种状态向量融合方法。以上算法可被总结为如下三种融合架构,如图3所示。
(a) 并行滤波
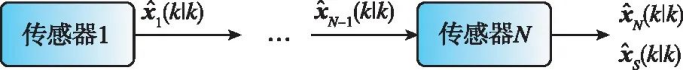
(b) 顺序滤波
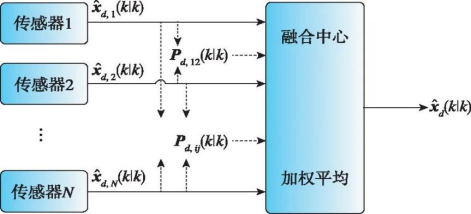
(c) 状态向量融合图3 三种不同的传感器融合架构
Fig.3 Illustration of different fusion architectures
图3(a)所示架构对应于观测融合方法中的并行滤波器和数据压缩滤波器。图3(b)所示架构对应于观测融合方法中的顺序滤波器。图3(c)所示架构为状态向量融合方法的示意图,传感器进行本地状态估计后,需要计算两两之间的估计误差协方差矩阵,再进行融合,数据融合可以在中心节点实现,也可以通过传感器网络的广播式通信在所有传感器本地实现。由于式(14)中的信息融合方法和联邦滤波器本质上也是一种状态向量融合方法,因此也可以由图3(c)中的架构描述。
2.2 未知相关性数据的融合——保守估计
由2.1节的讨论可知,传感器数据融合时需要获得所有传感器估计误差两两之间的相关性矩阵。但在实际的传感器网络中,由于通信带来的信息混合、相同的过程噪声以及传感器之间可能的位置关联,传感器间的估计误差的相关性是难以避免且通常是难以获得的[14],因此,表1提出的融合方法不易完美实现。对于高斯的未知误差间相关性的情况,S.J.Julier等[15]于1997年提出了协方差交叉(Covariance Intersection,CI)算法,给出了未知传感器间误差相关性时线性无偏融合估计误差协方差的最小上界,CI融合公式如下
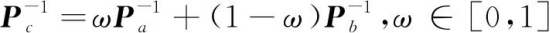 (15)
(15)
其中,ω是使得融合后协方差矩阵迹最小的常数,CI算法给出的融合误差协方差矩阵是对传感器间任意误差相关性的最小上界。Chen L.等[16]对CI算法进行了更直观的解读,提出了利用协方差椭圆对误差协方差矩阵进行可视化的方法。如图4所示,蓝色椭圆为两个传感器的估计误差;绿色椭圆为当两个传感器估计误差间不相关时的融合协方差,即当i≠j时,式(11)中的Pij=0;黑色椭圆为当传感器估计误差间相关性已知(取不同值)时的融合协方差;紫色虚线椭圆为当传感器间误差相关性未知的条件下,式(15)中的ω取不同值时的CI融合误差。文献[16]证明了两传感器在任意相关性时,融合误差椭圆均在蓝色的估计误差椭圆相交区域内。可以看出,CI给出的融合估计能对两个传感器协方差椭圆相交区域实现紧约束,因此,CI也被称作保守(Conservative)估计。
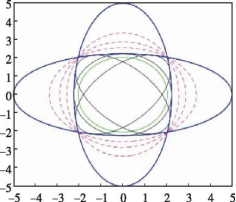
图4 已知相关性与未知相关性时的传感器融合误差椭圆
Fig.4 The ellipses for multisensor fusion under
known and unknown cross-covariance matrices
CI算法对于融合上界的计算是最优的,并且被M.B.Hurley用信息理论证明[17]可适用于任意的概率分布函数。但文献[14]也指出,CI算法对于两个以上的传感器融合时给出的误差协方差大于相交区域的紧约束,即CI算法对两个以上的未知相关性的多传感器融合结果不再是最小误差上界。并且CI算法本身也存在着优化计算量大、估计结果悲观保守等问题。为此,一些快速计算CI的方法[18-19]以及被称为最大椭圆(Largest ellipsoid)算法[20]的乐观估计方法被提出,但这种乐观估计方法也被证明存在估计缺陷。
总而言之,尽管CI算法不完美,但作为一种处理数据未知相关性的开创性经典方法,具有重要的理论与应用价值。目前,CI仍然是未知误差相关性时多传感器数据融合中的首选方法。T.Bailey等[21]还将保守估计思想推广至了未知的非高斯相关性的情况中。如今,能够解决未知误差相关性的保守融合估计方法已经在分布式状态估计的研究中被广泛地提出[22-26]。
3 一致性与分布式状态估计
早期对多传感器融合状态估计的研究[27-29]与文献[8]中类似,若要实现分布式状态估计,一个传感器节点需要获得网络中其他所有节点的信息,即所有传感器节点需要具备广播式的全局通信能力;亦或是像文献[13]中提出的算法,需要一个中心节点进行融合,如图2所示。正如文献[30]所述,这些方法只能被称作分散式(decentralized)状态估计,而非分布式(distributed)状态估计。一致性算法与代数图论的发展使得多传感器分布式状态估计架构成为可能。
3.1 一致性算法
在连通拓扑网络中,仅利用各个节点及其邻居的通信迭代实现网络中所有节点的信息或状态的一致被称为一致性问题。2004年,加州理工大学的R.Olfati-Saber等[31]解决了切换拓扑与延时网络的一致性问题(Consensus Problem),其核心公式为
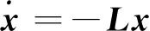 (16)
(16)
其中,L为网络的拉普拉斯矩阵;x为系统的状态。Xiao L.等[32]基于矩阵分析,于同年提出了计算平均一致性的快速线性迭代算法以及两种常用的加权方法:最大度加权和Metropolis加权方法,极大地方便了传感器网络对一致性方法的应用。核心公式为
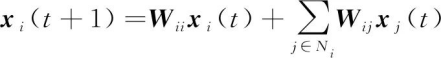 (17)
(17)
D.P.Spanos 等[33]证明了Xiao L.等在文献[32]中由矩阵理论导出的离散一致性算法,可由R.Olfati-Saber等在文献[31]中基于拉普拉斯矩阵的连续一致性思想推导而来,均可在迭代的稳态分布式地实现各个节点初始状态的平均一致性,即
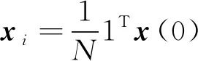 (18)
(18)
在传感器网络的通信拓扑联通条件下,平均一致性算法总能使各节点状态趋于一致,并且收敛于各个节点初始状态的平均值。一致性算法为分布式状态估计提供了强大的工具;拓扑网络能够仅利用节点与邻居的通信实现某种信息的一致性,解决了早期多传感器融合状态估计研究中对广播式通信或中心节点的依赖,可以使每个传感器分布式地得到相同的融合结果。
3.2 分布式状态估计算法
在随后的2005年,Xiao L.等[34]将平均一致性方法成功地应用于分布式传感器融合中,这是一种对观测对象状态为非随机观测量的分布式最大似然估计。同样在2005年,R.Olfati-Saber等在文献[31]的基础上提出了一致性滤波器[35],利用现代控制理论论证了这是一种低通滤波器并证明了其稳定性。基于这种一致性滤波器,R.Olfati-Saber等提出的分布式卡尔曼滤波器[36]是首个可扩展且完全分布式的滤波器,由低通一致性滤波器和带通一致性滤波器组成的微小嵌入式卡尔曼滤波器计算平均观测和平均逆协方差矩阵,理论上可以实现与集中式滤波相当的估计精度。然而,这种方法的缺陷在于,需要每个传感器拥有网络中节点总个数这一全局信息,并且只能应对所有传感器的观测矩阵都相同的场景,这是由其使用的低通滤波器的性质所决定的。
2007年,R.Olfati-Saber等[37]对一致性方法进行了全面而详细的总结,提供了网络一致性问题的理论框架和逻辑梳理,为后续多传感器分布式融合估计、协同控制和多智能体系统的发展奠定了坚实的基础。同年,R.Olfati-Saber等使用高通一致性滤波器[35,37]对其在文献[36]中提出的分布式滤波方法进行了改进[38],使其能适用于不同的传感器观测矩阵条件。此外,文献[38]还基于对传感器状态估计结果的一致性运算提出了两种分布式算法,被称为CE(Consen-sus on Estimates)算法。同为CE算法的还有F.S.Cattivelli等[39]提出的滤波策略。2009年,R.Olfati-Saber从最优估计角度出发[40],证明了以CE思想为基础的算法是一种次优估计。
对于分散式架构的最优估计,早在1988年,H.R.Hashemipour等[30]就基于卡尔曼滤波的信息形式提出了一种计算方法,但由于需要所有节点的信息,无法分布式工作。2008年,M.Kamgarpour等[42]基于卡尔曼滤波的信息形式以及文献[31-32]中的一致性算法,提出了一种分布式一致性卡尔曼滤波器,并证明了其收敛性。这种方法基于卡尔曼滤波的信息形式为
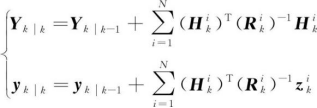 (19)
(19)
利用一致性算法,在传感器网络各个节点计算信息矩阵增量和信息向量增量的平均值
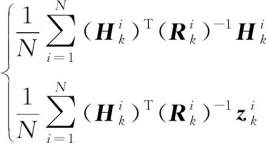 (20)
(20)
再用平均值乘以传感器总数N,就可以得到信息矩阵与信息向量的更新值,进而计算状态估计结果。由于从集中式卡尔曼滤波的信息形式推导得到,这种滤波器理论上具有与集中式滤波相同的估计精度,是一种最优估计[38,43],但需要每个传感器拥有传感器总数N这一全局信息,与算法[36]类似。在G.Battistelli等的研究中[44-45]被称为CM(Consensus on Mesurements)算法。
2011年,G.Battistelli等[46]提出了一种被称为信息一致性(Consensus on Information)的融合算法,该方法的出发点是利用KL散度量化两个概率密度函数之间的距离,即
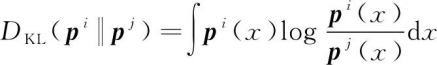 (21)
(21)
对于N个传感器的后验概率密度,再通过求解一个使平均KL散度最低的概率密度函数,得到融合后的概率密度
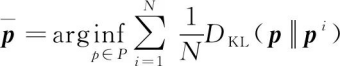 (22)
(22)
其计算结果是N个概率密度的几何平均值,对两个概率密度函数而言,该结果正是文献[17]中定义的广义协方差交叉融合(Generalized Covariance Intersection,GCI),以及文献[47]中讨论的广义Chernoff信息融合
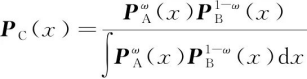 (23)
(23)
特别是在高斯概率密度时,式(22)的优化结果具有如下形式
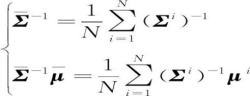 (24)
(24)
其中, 和
和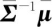 分别为融合后的信息矩阵与信息向量。该算法对各个传感器后验估计的信息向量与信息矩阵使用平均一致性算法,无需知道N的值,即可获得状态估计的均值及方差,所以该方法具有很强的拓扑以及通信容错能力,是一种理想的分布式融合方法。由式(24)不难看出,信息一致性算法(Consensus on Information)得到的协方差矩阵与2.2节中介绍的CI方法给出的协方差矩阵具有相同的形式,因此,信息一致性算法是一种保守估计。当传感器间估计误差不相关时,式(24)得到的状态均值与式(12)的状态向量融合结果相同,故该条件下信息一致性算法是对状态向量融合方法的一种无偏保守估计,实现了图3(c)中状态向量融合架构的分布式计算。G.Battistelli等在文献[44]的基础上提出了改进算法[45],并提高了算法的稳定性。
分别为融合后的信息矩阵与信息向量。该算法对各个传感器后验估计的信息向量与信息矩阵使用平均一致性算法,无需知道N的值,即可获得状态估计的均值及方差,所以该方法具有很强的拓扑以及通信容错能力,是一种理想的分布式融合方法。由式(24)不难看出,信息一致性算法(Consensus on Information)得到的协方差矩阵与2.2节中介绍的CI方法给出的协方差矩阵具有相同的形式,因此,信息一致性算法是一种保守估计。当传感器间估计误差不相关时,式(24)得到的状态均值与式(12)的状态向量融合结果相同,故该条件下信息一致性算法是对状态向量融合方法的一种无偏保守估计,实现了图3(c)中状态向量融合架构的分布式计算。G.Battistelli等在文献[44]的基础上提出了改进算法[45],并提高了算法的稳定性。
表2总结了本文介绍的自2004年以来的几种经典的多传感器分布式融合方法。此外,近年来还有很多研究着力于解决分布式状态估计中的其他问题,例如非线性、容错、异质传感器、数据不一致、信息冲突等问题,本文不详细解读。
表2 几种基于一致性的多传感器分布式融合方法
Tab.2 Several consensus-based distributed MSDF methods

4 结论
本文按照由集中式到分散式再到分布式状态估计的发展顺序,简要梳理了多传感器融合状态估计的发展。从直观的集中式滤波开始,以数据相关性问题为背景,调研了分散式、分布式滤波架构的发展历程,其中着重讨论了数据相关性在传感器数据融合中的重要性以及相应的已知相关性、未知相关性时的传感器数据融合方法(保守估计)。早期的研究需要融合中心或节点间的广播式全局通信能力,属于集中式或分散式滤波架构,如联邦滤波器等。随着2004年一致性问题的解决,大量经典、有效的分布式状态估计方法被提出,这些方法具备集中式所没有的鲁棒性、抗干扰能力、可靠性以及可扩展性,并且消耗更低的计算和通信资源。最后,本文介绍了一致性算法和一些经典的分布式方法,并在3.2节的末尾指出了信息一致性方法分布式地实现了状态向量融合的保守估计。对集中式、分散式和分布式状态估计方法的特点及其之间的联系总结如下:
1)集中式滤波架构:并行滤波、顺序滤波、数据压缩滤波。
以上三种集中式滤波方法也被称为观测融合,需要中心节点且需要所有传感器的观测值,三种方法在线性高斯系统且传感器同构时等价。
2)分散式滤波架构:状态向量融合、联邦滤波、信息融合。
以上三种基于分散式滤波架构的方法都能利用各个传感器自身的计算能力进行本地状态估计,也需要中心节点利用各个传感器的状态估计结果和协方差矩阵进行融合,与集中式滤波相比,分散式滤波将计算量分配到各个传感器节点中,降低了中心节点的计算负担。联邦滤波中,若所有子滤波器的状态均为公共状态,则状态融合精度与集中滤波器精度相同[48]。可以认为,联邦滤波通过将状态拆分为公共状态和私有状态,实现了状态向量融合方法在各个传感器状态估计不相关条件下异质传感器网络的融合状态估计。
3)基于一致性的分布式滤波架构:估计一致性、观测一致性、信息一致性。
分布式滤波架构基于一致性算法,在不依赖中心节点的情况下可以实现连通传感器网络的分布式状态估计,与集中式和分散式架构相比,分布式架构降低了计算量,并且提高了系统的鲁棒性,便于故障诊断。本文指出,信息一致性方法实质上是分布式地实现了状态向量融合的保守估计。
文章来源:中国指挥与控制学会